Question

The sum of 3 consecutive integers is less than or equal to 15 what is one possible set of three integers to satisfy this inequality hint let n represent the first number so then the next number would be n+1 and so on

Answer 1

Step 1

Let the first consecutive integer be n

Then the second will be n+1

The third will be n+2

Step 2

Write an inequality for the problem

`n+n+1+n+2\leq15`

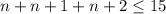
Step 3

Solve the inequality

`\begin{gathered} 3n+3\leq15 \\ 3n\leq15-3 \\ 3n\leq12 \\ (3n)/(3)\leq(12)/(3) \\ n\leq4 \end{gathered}`

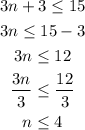
Step 4

Find the possible set of three integers to satisfy the inequality.

`\begin{gathered} n=4---\text{ first integer} \\ n+1=4+1=5---\text{ second integer} \\ n+2=4+2=6---\text{ Third integer} \\ \text{check} \\ 4+5+6\leq15 \\ \text{Hence the set of thr}ee\text{ integers are; }\mleft\lbrace4,5,6\mright\rbrace \end{gathered}`

One possible set of three integers that satisfy the inequality is;

{4,5,6}