Question

The parallel circuit at the right depicts two resistors connected to a voltage source. The voltage source (ΔVtot) is a 12-V source and the resistor values are 7.4 Ω (R1) and 3.9 Ω (R2).a. Determine the equivalent resistance of the circuit. b. Determine the current in each branch resistor:Current in R1 = Current in R2 = c. Determine the total current in the circuit.

Answer 1

Given:

Two resistors are connected in parallel.

The resistance of resistor 1 is

`R1=\text{ 7.4}\Omega`

The resistance of resistor 2 is

`R2\text{ = 3.9 }\Omega`

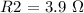
The value of the voltage source is

`\Delta V_(tot)=\text{ 12 V}`

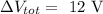
Required:

(a)The equivalent resistance of the circuit.

(b) The current in each branch of the resistor.

(c) The total current in the circuit.

Step-by-step explanation:

(a) In a parallel circuit, the equivalent resistance can be calculated as

`\begin{gathered} (1)/(R_(eq))=(1)/(R1)+(1)/(R2) \\ =(1)/(7.4)+(1)/(3.9) \\ R_(eq)=\text{ 2.55 }\Omega \end{gathered}`

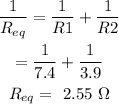
(b) In a parallel circuit, the voltage across each resistor is the same.

The current through the resistor R1 can be calculated according to Ohm's law

`\begin{gathered} I_(R1)=(V)/(R1) \\ =(12)/(7.4) \\ =1.62\text{ A} \end{gathered}`

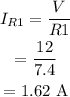
The current through the resistor R2 can be calculated as

`\begin{gathered} I_(R2)=(V)/(R2) \\ =(12)/(3.9) \\ =3.08\text{ A} \end{gathered}`

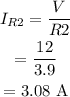
(c) The total current in the circuit is the sum of the current through each branch.

Thus, the total current can be calculated as

`\begin{gathered} I=I_(R1)+I_(R2) \\ =(12)/(7.4)+(12)/(3.9) \\ =\text{ 4.7 A} \end{gathered}`

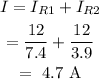
Final Answer:

(