Question

Find the first term of the arithmetic sequence in which a76 = 375 and the common difference is 4.8.

Answer 1

Given:

The expression for arithmetic expression is given as,

`a_(76)=375`

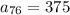
The common difference is d = 4.8.

The objective is to find the first term of the series.

Step-by-step explanation:

The general formula for the nth term of an arithmetic progression is,

`a_n=a+(n-1)d\text{ . . . . .(1)}`

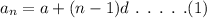
Here, n represents the number of terms, a represents the first term

By comparing the given expression with equation (1),

`n=76`

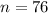
To find a:

On plugging the given values in equation (1),

`375=a+(76-1)4.8`

On further solving the above equation,

`\begin{gathered} 375=a+(75)4.8 \\ 375=a+360 \\ a=375-360 \\ a=15 \end{gathered}`

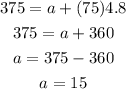
Hence, the first term of the arithmetic sequence is 15.