To answer this question, we can identify the pair of values on the graph as follows:
x y
5 118
7 330
15 424
17 680
22 770
26 910
28 750
However, the values are approximated since the only given values are:
(5, 118), (15, 424), (22, 773), and we got them from the above graph.
If we use technology to find the regression line for these values, we have that:
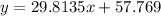
And we can see this line equation as follows:
Then, to find how many toy drift cars Grandpa Sean will probably sell in the 40th year, we need to substitute the value of x = 40 into the regression line as follows:
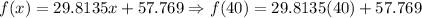
Then, we have that:

Therefore, Grandpa Sean will probably sell, approximately, about 1250 toy drift cars in the 40th year (using all of the given values in the graph).