Question

Type the correct answer in each box. Use numerals instead of words. Consider the systems of equations below. System A System B System C I2 + y2 = 17 y = 12 - 70 + 10 = y = – 2229 - 1 2 3 - y = -65 + 5 &r - y = -17 Determine the number of real solutions for each system of equations. System A has real solutions. System B has real solutions. System C has real solutions.

Answer 1

A) Given:

`\begin{gathered} x^2+y^2=17\ldots\ldots\ldots\text{.}(1) \\ y=-(1)/(2)x\ldots\ldots\ldots\ldots(2) \end{gathered}`

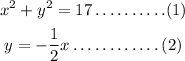
To find: The number of real solutions

Step-by-step explanation:

Substitute equation (2) in (1), we get

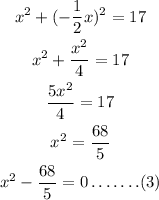
`\begin{gathered} x^2+(-(1)/(2)x)^2=17 \\ x^2+(x^2)/(4)=17 \\ (5x^2)/(4)=17^{} \\ x^2=(68)/(5) \\ x^2-(68)/(5)=0\ldots\ldots.(3) \end{gathered}`

Here,

`a=1,b=0,\text{ and c=-}(68)/(5)`

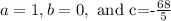
So, the discriminant is,

`\begin{gathered} \Delta=b^2-4ac \\ =0-4(1)(-(68)/(5)) \\ =54.4 \\ >0 \end{gathered}`

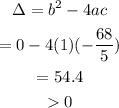
Since the discriminant is greater than zero.

Hence, it has two real solutions

Final answer:

System A has two real solutions.