We know that
• The mass of the ball is 10kg.
,
• The initial velocity of the ball is 9m/s.
,
• The mass of the man is 130kg.
,
• The initial velocity of the man is null (stationary).
,
• The final velocity of the ball is 5m/s.
To find the final velocity of the person, we have to use the law of conservation of momentum.
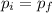
Where p = mv. Using all the given information, we have
![\begin{gathered} m_{^{}_(ball)}v_{i_(ball)}+m_{_(man)}v_{i_(man)}=m_{\text{ball}}v_{f_(ball)}+m_(man)v_{f_(man)}_{} \\ 10\operatorname{kg}\cdot9m/s+130\operatorname{kg}\cdot0=10\operatorname{kg}\cdot5m/s_{}_{}+130\operatorname{kg}\cdot v_{f_(man)} \end{gathered}]()
Then, we solve for v
![\begin{gathered} 90\operatorname{kg}\cdot m/s=50\operatorname{kg}\cdot m/s+130\operatorname{kg}\cdot v_{f_(man)} \\ \frac{90\operatorname{kg}\cdot m/s-50\operatorname{kg}\cdot m/s}{130\operatorname{kg}}=v_{f_(man)} \\ v_{f_(man)}=\frac{40\operatorname{kg}\cdot m/s}{130\operatorname{kg}}\approx0.31m/s \end{gathered}]()
Therefore, the velocity of the person after the ball bounces off him is 0.31 meters per second, approximately.