Question

Which pair of functions are inverses of each other?A. f(x) = 5 + 6 and g(x) = 5x - 6B. f(x) = { and g(x) = 6x3C. f(x) = 7x - 2 and g(x) = 42D. f(x) = - 2 and g(x) = -2

Answer 1

To find the pair of functions that are inverses of each other, we should check through the options.

Option A

`\begin{gathered} f(x)\text{ = }(x)/(5)\text{ + 6} \\ g(x)\text{ = 5x -6} \end{gathered}`

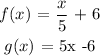
First, we set f(x) = y. Thus:

`y=\text{ }(x)/(5)\text{ + 6}`

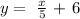
Then, we swap the variables:

`x\text{ = }(y)/(5)\text{ + 6}`

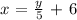
Make y the subject of formula:

`\begin{gathered} x\text{ = }(y)/(5)\text{ + 6} \\ (y)/(5)\text{ = x -6} \\ y\text{ =5x -30} \end{gathered}`

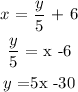
But:

`g(x)\text{ }\\e\text{ 5x -30}`

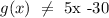
Hence, option A is incorrect

Option B

`\begin{gathered} f(x)\text{ =}\frac{\sqrt[3]{x}}{6} \\ g(x)=6x^3 \end{gathered}`

Set f(x) = y. Thus:

`y\text{ = }\frac{\sqrt[3]{x}}{6}`

Swap the variables:

`x\text{ = }\frac{\sqrt[3]{y}}{6}`

Make y the subject of the formula:

`\begin{gathered} 6x\text{ = }\sqrt[3]{y} \\ \text{Cube both sides} \\ (6x)^3\text{ = y} \\ y\text{ = }216x^3 \end{gathered}`

But:

`g(x)\text{ }\\e216x^3`

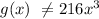
Hence, Option B is incorrect

Option C:

`\begin{gathered} f(x)\text{ = }7x\text{ -2} \\ g(x)\text{ = }\frac{x\text{ + 2}}{7} \end{gathered}`

Set f(x) = y. Thus:

`y\text{ = 7x - 2}`

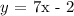
Swap the variable:

`x\text{ = 7y -2}`

Make y the subject of formula:

`\begin{gathered} x\text{ + 2 = 7y} \\ 7y\text{ = x +2} \\ \text{Divide both sides by 7} \\ (7y)/(7)\text{ = }(x+2)/(7) \\ y\text{ = }(x+2)/(7) \end{gathered}`

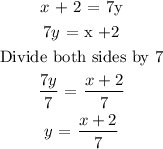
But :

`g(x)\text{ = }(x+2)/(7)`

Hence, option C is correct

Option D

`\begin{gathered} f(x)\text{ = }(5)/(x)\text{ -2} \\ g(x)\text{ =}(x+2)/(5) \end{gathered}`

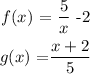
Set y =f(x). Thus:

`y\text{ = }(5)/(x)\text{ -2}`

Swap the variables:

`x\text{ = }(5)/(y)\text{ -2}`

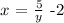
Make y the subject of formula: