Answer:
67 bags of sand
Step-by-step explanation:
First, we need to calculate the area of the path. So, this area can be calculated as the difference between the area of the circle with a diameter of 36 yd and the area of the circle with 28 yd.
The area of a circle can be calculated as:

Where π is 3.14 and r is the radius of the circle.
The radius of a circle is half the diameter. So, the radius of the circle with a diameter of 36 yd is 18 yd and its area is:
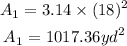
In the same way, the radius of the circle with a diameter of 28 yd is 14 yd and its area is equal to:
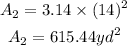
Then, the area of the path is equal to:
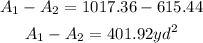
Now, the number of bags of sand can be calculated as:
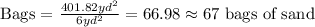
Because each bag of sand covers 6 yd².
Therefore, the gardener needs 67 bags of sand