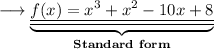To Find :-
- To write a polynomial function f(x) x) (in factored form and standard form) of least degree that has rational coefficients, a leading coefficient of 1, and -4, 1, and 2 as zeros.
Solution :-
Given zeros are ,
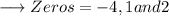
Since there are three zeroes , the polynomial will be a cubic polynomial .
We know that if ,
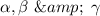 are the zeros of the cubic polynomial then , we can write the polynomial as ,
are the zeros of the cubic polynomial then , we can write the polynomial as ,
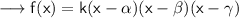
where k is constant ,
Hence here ,
Hence here the polynomial can be written in factored form as ,
![\sf\longrightarrow f(x) =1 [ x -(-4)] ( x-1)(x-2)\\](https://img.qammunity.org/2023/formulas/mathematics/high-school/ixdmi0ctdhskh4p9fdaw43nsaqp3t4wiuh.png)
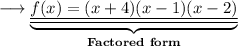
Again we know that the Standard form of a cubic polynomial is ,

Now to find in standard form multiply the all three , as ,
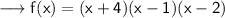
![\sf\longrightarrow f(x) = [ x ( x-1) +4(x-1)] (x-2)\\](https://img.qammunity.org/2023/formulas/mathematics/high-school/7r0vyo27xly72xbo53izzfhy8twb970m8t.png)
\\](https://img.qammunity.org/2023/formulas/mathematics/high-school/2qh2azi75jzqm6ygkjw31f0w3g08xnkp9j.png)

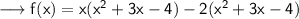
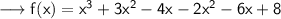
Add like terms ,