Step-by-step explanation:
Let's call A the ounces of solution A and B the ounces of solution B.
If the scientist wants to obtain 120 ounces, then:
A + B = 120
On the other hand, the final mixture should be 60% salt and solution A is 30% salt and solution B is 80% salt, so:
0.6(A + B) = 0.3A + 0.8B
So, we can solve for A as:
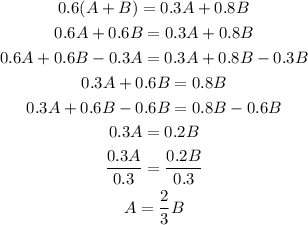
Then, replacing A by (2/3)B on the first equation, we get:

Finally, A is equal to:
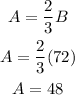
Therefore, she should use 48o
Let[