To find:
The equation of the tangent line to the function y = 2x at point (1,2).
Solution:
The given function is y = 2x. Now, take a point through which the given function is passing through i.e., (2,4).
Now, find the slope of the line:
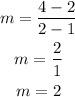
The slope of the function is m = 2. The given function represents a line whose slope is same at every point.
Now, at (1,2), the slope is 2. So, the equation of the tangent line is:
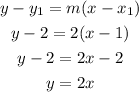
Thus, the equation of the tangent line is y=2x.