Question

the polynomial of degree 3 p x have the root of Multiplicity 2 at x equals 3 and a root of Multiplicity 1 at x equals negative 5 the Y intercept is y equals -27 find a formula for p x

Answer 1

P(x) = (x - 3 )^2 (x + 5) - 72

Explanation:

We are told that the polynomial has a root of multiplicity 2 at x = 3. This means (x - 3)^2 is present in the polynomial. Alos, the root at x = -5 has a multiplicity 1, meaning (x + 5) is also present; therefore, we can write our polynomial as

`P(x)=(x-3)^2(x+5)`

Now, the y-intercept of P(x) is -27, meaning

`P(0)=-27`
`\begin{gathered} P(0)=(0-3)^2(0+5)+c=-27 \\ 9\cdot5+c=-27 \\ 45+c=-27 \\ \boxed{\therefore c=-72.} \end{gathered}`

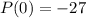
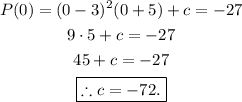
Hence, the equation for the polynomial is