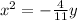Question

Write an equation for the parabola with vertex at the origin.

Answer 1

in this problem, we need to find the equation of a parabola given the vertex and (0,0) and the focus at (0,-1/11).

First, let's look at the standard form a parabola. This equation can sometimes vary depending on the curriculum you use.

`\begin{gathered} (x-h)^2=4p(y-k)\text{ for a parabola with a vertical axis.} \\ \\ (y-k)^2=4p(x-h)\text{ for a parabola with a horizontal axis.} \end{gathered}`

This is what it looks like when you see the different parts of a parabola on a graph:

Notice the focus lines up with the vertex, so this parabola has a vertical axis. Since our Focus has an x-value of 0 and a y-value of -1/11, we are working with a vertical parabola that opens down.

The focus is always going to be inside the parabola.

Since this parabola opens down, and it has a vertex at (0,0), we can use a modified equation:

`x^2=4py`

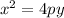
From the equation, the "p" value represents the distance from the vertex to the directrix and the focus.

In this case:

`p=|(-1)/(11)|=(1)/(11)`

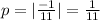
So now we have the equation

`\begin{gathered} x^2=4((1)/(11))y \\ \\ x^2=(4)/(11)y \end{gathered}`

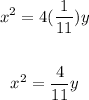
And since the parabola opens down, we simply include a negative with our equation:

`x^2=-(4)/(11)y`