In order to calculate the acceleration of the system, let's consider both masses as one object, and use the Second Law of Newton (considering that the blocks are moving down):
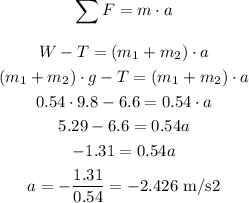
So the acceleration is 2.426 m/s² upwards.
The tension in the lower rope can be calculated using the Second law just in the lower block:
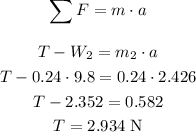
The tension in the lower rope is equal to 2.934 N.