Answer:
$
Explanation:
The formula for compound interest is given below:

For the given problem:
• The amount Alex deposited, P = $6,000
,
• Annual Percentage Rate = 1.2% = 1.2/100 = 0.012
,
• Time, t = 6 years
,
• The number of compounding periods, n = 12 (Monthly)
Substitute these values into the formula above:
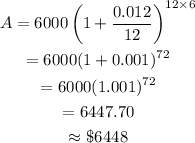
The amount in 6 years is $6,448 (correct to the nearest dollar).