Question

Click an item in the list or group of pictures at the bottom of the problem and holding the button down drag it into thecorrect position in the answer box Release your mouse button when the tem s place you change your mind dragthe item to the trashcan click the trashcan to clear all your answerIndicate the equation of the given line in standard forThe line that contains the point Q-2 and is parallel to the line whose ecuation1 - 4 - 2/3 (x-3)

Answer 1

Given the equation of a line:

`y\text{ - 4 = }(2)/(3)\text{ (x - 3)}`

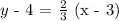
Step 1: Obtain the slope of the given line

Writing this equation in the standard slope-intercept form, we will obtain the following

`\begin{gathered} y\text{ - 4 = }(2)/(3)x\text{ - }(2)/(3)*3 \\ \\ y\text{ - 4 =}(2)/(3)x\text{ - 2} \end{gathered}`

`y\text{ =}(2)/(3)x\text{ - 2+ 4}`

`y\text{ = }(2)/(3)x\text{ + 2}`

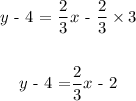
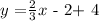
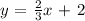
If we compare this to y = mx + b, where m is the slope and b the intercept

the slope of the line is

`(2)/(3)`

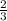
Step 2: Getting the equation of the line,

The equation of a line given a slope is given by

`\text{slope = }(y-y_1)/(x-x_1)`

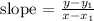
where x1 and y1 are the coordinates of the points parallel, in this case

x1 =1, y1 = -2

`(2)/(3)\text{ =}\frac{y-\text{ (-2)}}{x\text{ -1}}`

`(2)/(3)\text{ =}\frac{y\text{ +2}}{x\text{ - 1}}`

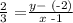
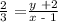
Cross multiplying

2 (x - 1) = 3 (y +2)

expand the parenthesis

2x - 2 = 3y + 6

3y = 2x -2 -6

3y = 2x - 8

Divide both sides by 3

`y\text{ = }(2)/(3)x\text{ - }(8)/(3)`

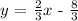
Answer is y = 2x/3 - 8/3