Question

Please solve number 9. Solve each equation by completing the square. Simplify all irrational and complex solutions

Answer 1

Given

Solve using completing the square

`x^2-8x+4\text{ =0}`

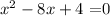
Step 1

Keep x terms on the left and move the constant to the right side

by subtracting it on both sides

`x^2-8x=-4`

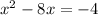
Step 2

Take half of the x term and square it

`(-8\text{ }*(1)/(2))^2=16`

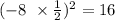
Step 3

Then add the result (16) to both sides

`x^2-8x+16=-4+16`

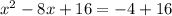
Step 4

Rewrite the perfect square on the left

`(x-4)^2=-4+16`

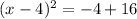
and combine terms on the right

`(x-4)^2=12`

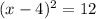
Step 5

Take the square root of both sides

`x-4=\pm\sqrt[]{12}`

Simplify the Radical

`x-4=\pm2\sqrt[]{3}`

Step 6

Isolate the x on the left side and

solve for x

`x=4\pm2\sqrt[]{3}`

therefore

`\begin{gathered} x=4+2\sqrt[]{3} \\ \\ x=4-2\sqrt[]{3} \end{gathered}`

which becomes

x = 7.4641

x = 0.535898