Question

Consider the following inequality:[x-1 < 0Step 1 of 2: Solve the absolute value inequality and express the solution in interval notation.AnswerHow to enter your answer (opens in new window)KeypadKeyboard ShortcutsSelecting a radio button will replace the entered answer value(s) with the radio button value. If the radiobutton is not selected, the entered answer is used.O No Solution

Answer 1

We are asked to solve the following:

`|x|-1<0`

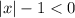
Step-by-step explanation

[tex]\begin{gathered} |x|-1<0 \\ \text{Add 1 to both sides} \\ |x|<1 \\ \\ \text{The real value of }x\text{ without the absolute value, can either be negative or positive.} \\ \text{ Since the absolute value of x which is always positive is less than 1, then, if the real value of }x \\ is\text{ actually positive, then, } \\ x<1. \\ (NOTE\colon\text{ This implies that if x is positive, then, its either 0 or a decimal between 0 and 1)} \\ \text{However, if }x\text{ is actually negative, then, it would be true that }x<1\text{ but }x>-1\text{ because the magnitude of }x\text{ is a} \\ \text{decimal between 0 and 1} \\ \text{Thus, another solution to the problem is:} \\ x>-1\implies-1

Final Answer

The answer is

[tex]\begin{gathered} -1