Question

What is the volume of the cone below. Round to the nearest whole number.

Answer 1

The volume of the cone is 3,434 cubic km

Explanation:

The volume of a cone is calculated using the formula:

`V=(1)/(3)\pi r^2h\text{ where }\begin{cases}r={Radius} \\ h={Perpendicular\;Height}\end{cases}`

From the given diagram, the diameter of the cone = 27 km.

`Radius,r=(Diameter)/(2)=(27)/(2)=13.5\;km`

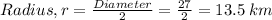
Next, we find the perpendicular height of the cone using the Pythagorean Theorem:

`\begin{gathered} h^2+13.5^2=22.5^2 \\ h^2=22.5^2-13.5^2 \\ h=√(22.5^2-13.5^2) \\ h=18\text{ km} \end{gathered}`

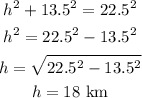
Substitute r=13.5, h=18, and π=3.14 into the formula:

`\begin{gathered} V=(1)/(3)*3.14*13.5^2*18 \\ =3433.59 \\ \approx3434\;km^3 \end{gathered}`

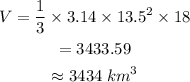
The volume of the cone is 3,434 cubic km (to the nearest whole number).