Answer:
7.06 units
Step-by-step explanation:
The given side lengths are indicated in the diagram below:
Using similar triangles, we have:
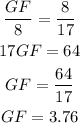
Next, apply Pythagorean Theorem to triangle DGF.
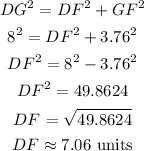
The length of DF is approximately 7.06 units (to the nearest hundred).