P(at least one Physics instructor) = 0.9848
1) Since we have 5 chemistry instructors and 6 Physics ones then we need to resort to some Combination so that we can find the Probability of "At least one of them being a Physics Instructor.
2) Let's write out the following, Notice that the committee is made up by
4 people. Since we want the Probability of At least one, let's calculating subtracting this combination from 1, since "at least one" comprehends:
1, 2, 3, and 4 Physics Instructor.
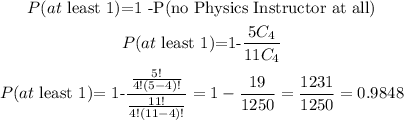
Notice also that if we had calculated: P(1), P(2), P(3), and P(4) physics instructor most likely we could have committed a mistake. So for these cases, "at least 1" the best scenario is to subtract from 1 (the whole)
3) Hence, the Probability of picking a committee with at least 1 Physics Instructor is 0.9848, i.e. it is very unlikely that in this committee there is not at least one Physics Instructor.