Question

A survey approximates the number of Americans that are age 65 and older and projects that by the year 2050, approximately 82.2 million Americans will be at least 65. The bar graph shows the estimated number of Americans with projected figures for the year 2020 and beyond.A graphing calculator screen displays an exponential function that models the U.S. population age 65 and over, y, in millions,x years after 1899. Use this information to solve (a)-(d) below.ExpRegy = a*b^xClick the icon to view the bar graph.a = 3.4854891603b= 1.022941093a. Explain why an exponential function was used to model the population data.OA. An exponential function was used because exponential functions are always more accurate than linear functions.B. An exponential function was used because the population is always modeled using exponential functions.OC. An exponential function was used because the data in the bar graph is increasing more and more rapidly.

Answer 1

An exponential function was used to model the population data because it accurately represents the growth shown in the bar graph. The exponential function accounts for the increasing trend of the estimated number of Americans age 65 and older projected into the future.

Step-by-step explanation:

An exponential function was used to model the population data because exponential functions are well-suited for representing growth or decay that occurs at a constant percentage rate. In this case, the function models the U.S. population age 65 and over, with the variables 'y' representing the population size in millions and 'x' representing the number of years after 1899.

Using the given equation, y = a * b^x, where 'a' is the initial population size and 'b' is the constant multiplier, we can see that as 'x' increases, the population size 'y' will grow exponentially. This aligns with the increasing trend shown in the bar graph, where the estimated number of Americans age 65 and older is projected to increase over time.

Therefore, option C is the correct answer: An exponential function was used because the data in the bar graph is increasing more and more rapidly.

Answer 2

ANSWER and EXPLANATION

(a) An exponential function was used to model the population data.

We notice that from the bar graph, the population increases very quickly as the number of years after 1899 increases.

This shows that the population data is increasing rapidly; hence, an exponential function was used.

The answer is option C.

(b) The general form of an exponential function is given as:

`y=a*b^x`

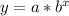
where a = initial value; b = exponential factor

We are given the values of a and b, so, to find the function for the population data, substitute the approximated values of a and b into the function:

`y=3.485*(1.023)^x`

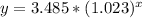
That is the function.

(c) To find the number of Americans aged 65 and over in 2010, we have to first find how many years after 1899 2010 is:

`\begin{gathered} 2010-1899 \\ \\ 111 \end{gathered}`

Now, using the model in b, solve for y when x is 111:

`\begin{gathered} y=3.485*(1.023)^(111) \\ \\ y=43.5\text{ million} \end{gathered}`

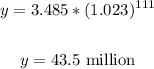
According to the bar chart, we see that in 2010, it is estimated that there will be 45.3 million people aged 65 and over.

We see that the rounded value obtained above is less than the value displayed by the bar graph by a value of:

`\begin{gathered} 45.3-43.5 \\ \\ 1.8\text{ million} \end{gathered}`

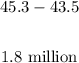
Hence, the rounded value underestimates the 2010 population by 1.8 million.

(d) To find the number of Americans that will be age 65 and over in 2020, first, find how many years after 1899 that 2020 is:

`\begin{gathered} 2020-1899 \\ \\ 121\text{ years} \end{gathered}`

Now, solve for y when x is 121:

`\begin{gathered} y=3.485*(1.023)^(121) \\ \\ y=54.6\text{ million} \end{gathered}`

That is the estimated number of Americans that will be age 65 and over in 2020/