Question

Elijah invested $610 in an account paying an interest rate of 4.1% compoundedannually. Assuming no deposits or withdrawals are made, how long would it take, to the nearest year, for the value of the account to reach $900?

Answer 1

Use the formula for the compounding of interest

`A=P(1+(r)/(n))^(n\cdot t)`

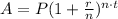
since the compounding is annually, n=1 which reduces the formula to

`A=p(1+r)^t`

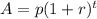
use values for

A=900

p=610

r=0.041

solve the equation for t

`900=610\cdot(1+0.041)^t`
`(900)/(610)=(1.041)^t`
`\ln ((900)/(610))=\ln (1.041)^t`

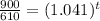
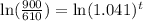
apply the log properties

`\ln ((900)/(610))=t\cdot\ln (1.041)`

solve for t

`\begin{gathered} t=(\ln ((900)/(610)))/(\ln (1.041)) \\ t\approx9.68 \end{gathered}`

It would take about 10 years to reach 900 in the account