Given:
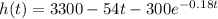
Find-:
(1)
Velocity at the instant when t = 6 sec.
(2)
The time when velocity is -45 meter per sec
Explanation-:
Velocity is define as a:
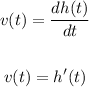
The value of the h'(t) is:
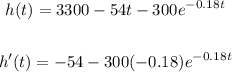
Value is:
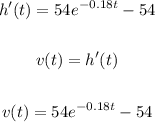
At t=6 velocity is:
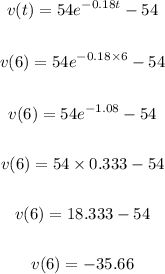
At t=6 velocity is -35.66 meters per sec.
(b)
Velocity is -45 meter per second then time is:
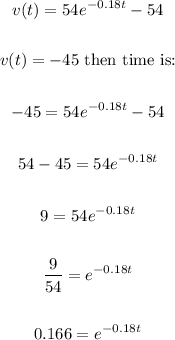
Taking log both side then,
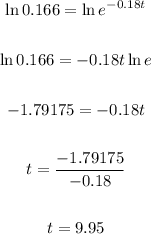
So, the time is 9.95 second