hello
solve the first problem, we are to find the missing angle
to solve for x, i had to make up new characters to find missing sides
first of all, let's solve for y
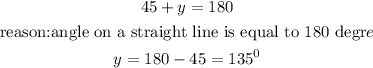
let's use this knowledge to solve for z

note: z= 45, we can as well use opposite angles are equal theorem
we should solve for angle a now
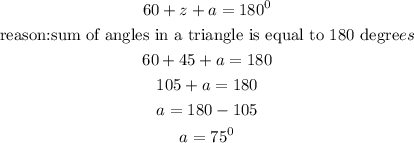
we ca use the knowledge of a to solve for b
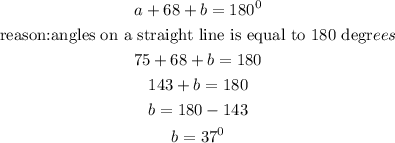
let's use the value of b to solve for c
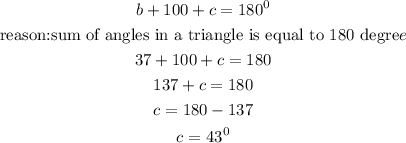
finally, we can solve for x
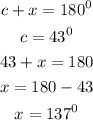
the value of the unknown angle is equal to 137 degrees