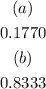Step-by-step explanation:
We are given a bag of marbles and the conditions are;
5 blue marbles
11 red marbles
14 green marbles
Total of 30 marbles.
To calculate the probability of an event such as the one in this experiment, we shall use the formula;
![P[E]=\frac{Number\text{ of required outcomes}}{Number\text{ of all possible outcomes}}](https://img.qammunity.org/2023/formulas/mathematics/college/yyxout6mmsixrxrn3m64v9rcy22xdisewy.png)
Marbles are now chosen at random;
The probability of getting a red marble will be;
![P[red]=(11)/(30)](https://img.qammunity.org/2023/formulas/mathematics/college/mov8l3956olqyh3a93ouc7hu0g44jpbyjw.png)
Note that the number of all possible outcomes is 30 since there are 30 marbles in all (regardless of the color).
The probability of getting a green marble would now be dependent on a total of 29 marbles. Note that 1 marble has been chosen already, which means our experiment now has a total possible outcome of 29.
![P[green]=(14)/(29)](https://img.qammunity.org/2023/formulas/mathematics/college/gdr16l9lmixbdn7w9qnozzibqptvewzlnw.png)
At this point we should note that when we need to find the probability of one event and then another, what we have is a product of probabilities.
Therefore, the probability of getting a red and then a green marble when two marbles are chosen, will be;
![P[red]* P[green]](https://img.qammunity.org/2023/formulas/mathematics/college/a6m6bscr07wj5hpbe2c6uzlfz803crbgjo.png)
![P[red]\text{ and }P[green]=(11)/(30)*(14)/(29)](https://img.qammunity.org/2023/formulas/mathematics/college/lkfnhnl4l75f645yytq9ezoz95u66vmbim.png)
![P[red]\text{ and }P[green]=(154)/(870)](https://img.qammunity.org/2023/formulas/mathematics/college/yt52y3j756epxouf436tmgl5ran7abfwx8.png)
![P[red]\text{ and }P[green]=(77)/(435)](https://img.qammunity.org/2023/formulas/mathematics/college/nbe7tl5t6zpwk0ct5wtzrk0h7fzeyvkywm.png)
![P[red]\text{ and }P[green]=0.1770](https://img.qammunity.org/2023/formulas/mathematics/college/bhot2cwu2ycjaz2whvabgsxxxuayrjvp93.png)
The probability of getting a red or a green marble when one marble is chosen is calculated as follows;
![P[red]\text{ Or }P[green]](https://img.qammunity.org/2023/formulas/mathematics/college/enpf2d8jva8gt5zgpkg2v4zg9fsozvv1ba.png)
The probability of one event or the other occuring is simply an addition of probabilities.
Therefore, we would have;
![P[red]=(11)/(30)](https://img.qammunity.org/2023/formulas/mathematics/college/mov8l3956olqyh3a93ouc7hu0g44jpbyjw.png)
![P[green]=(14)/(30)](https://img.qammunity.org/2023/formulas/mathematics/college/thp535gspp56wl2hklhsy4jnvaeiomafcx.png)
Take note that one marble is drawn and NOT two like the first experiment.
![P[red]+P[green]=(11)/(30)+(14)/(30)](https://img.qammunity.org/2023/formulas/mathematics/college/385tnnevj29sj7gh8o7a403hrc7nqyvrg4.png)
![P[red]+P[green]=(25)/(30)](https://img.qammunity.org/2023/formulas/mathematics/college/n0ip8ve5idrqv1lzvv2vapw366k1vsm7dy.png)
![P[red]+P[green]=(5)/(6)](https://img.qammunity.org/2023/formulas/mathematics/college/l6r85urlivya33rlxikijwc9dvnx3afdxc.png)
![P[red]+P[green]=0.8333](https://img.qammunity.org/2023/formulas/mathematics/college/z3bmzznznlot43qha6m2jgokd9zsmtz209.png)
ANSWER: