Question

A cockroach of mass m lies on the rim of a uniform disk of mass 5m that can rotate freely about its center like a merry-go-round. Initially the cockroach and disk rotate together with an angular speed of 0.26 rad/s. Then the cockroach walks half-way to the center of the disk.A. What is the angular speed of the cockroach-disk system after the cockroach walks to its final position? B. What is the ratio Kf/Ki of the new rotational kinetic energy of the system to its initial rotational kinetic energy?

Answer 1

Given data:

The mass of cockroch is m.

The mass of disk is 5m.

The initial speed of cockroch and disk is ω=0.26 rad/s.

Considering the radius of the disk is r, then the halfway radius of the disk will be r/2.

Part (a)

The final angular velocity can be calculated as,

`\begin{gathered} (I+I)\omega=(I+I)_(final)\omega^(\prime) \\ (mr^2+(1)/(2)5mr^2)0.26=(m((r)/(2))^2+(1)/(2)5m((r)/(2))^2)\omega^(\prime) \\ 0.91=0.875\omega^(\prime) \\ \omega^(\prime)=1.04\text{ rad/s} \end{gathered}`

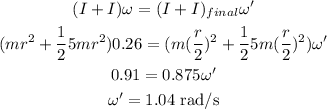
Thus, the final speed is 1.04 rad/s.

Part (b)

The ratio of kinetic energy can be calculated as,

`\begin{gathered} (K_f)/(K_i)=((1)/(2)(I+I)_(final)\omega^2)/((1)/(2)(I+I)\omega^2) \\ (K_f)/(K_i)=\frac{(1)/(2)(m((r)/(2))^2+(1)/(2)5m((r)/(2))^2_{})(1.04)^2}{(1)/(2)(mr^2+(1)/(2)5mr^2)(0.26)^2} \\ (K_f)/(K_i)=7.42 \end{gathered}`

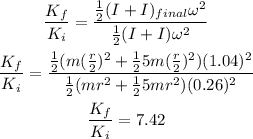
Thus, the ratio of kinetic energy is 7.42.