Question

Factor 3x^2y^2 - 6xy^2

Answer 1

From the binomial:

`3x^2y^2-6xy^2`

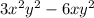
We can factor out the GCF by factoring out the GCF of the coefficients, and the lowest power of each variable.

The GCF of 3 and 6 is 3.

The lowest power of x is 1.

The lowest power of y is 2.

Then, we can factor out:

`3xy^2`

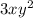
Multiply each term by:

`(3xy^2)/(3xy^2)`

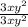
Which does not change the meaning of the expression, since that fraction is equal to 1:

`\begin{gathered} 3x^2y^2-6xy^2=3x^2y^2*^{}(3xy^2)/(3xy^2)-6xy^2*^{}(3xy^2)/(3xy^2) \\ =3xy^2(\frac{3x^2y^2^{}}{3xy^2}-(6xy^2)/(3xy^2)) \\ =3xy^2(x-2) \end{gathered}`

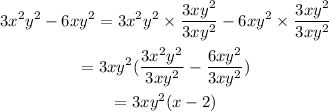
Therefore:

`3x^2y^2-6xy^2=3xy^2(x-2)`