We are given the following system of linear equations
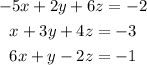
Let us solve the given system of equations.
First, let us find the determinant.
The determinant is given by
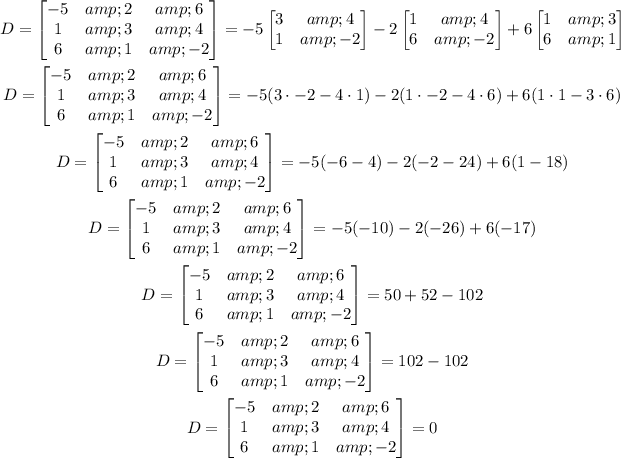
As you can see, the determinant of the matrix is 0
This means that the given system of equations has no solution.