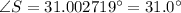Question

Find the value of Angle S and round it off to the nearest Tenth.

Answer 1

From the figure, the only information given is the measure of its Hypotenuse and the Adjacent Side. The triangle also has 90 degrees interior angle, thus, this triangle is a right triangle and we can apply this Trigonometric Function:

`\text{Cosine(}\Theta)\text{ = Cosine (}\angle\text{S) = }\frac{Adjacent\text{ Side}}{Hypotenuse}`

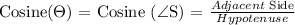
Given the following information:

Hypotenuse = 7

Adjacent Side = 6

Let's now find the value of Angle S.

`\text{Cosine(}\Theta)\text{ = Cosine(}\angle S)=\frac{Adjacent\text{ Side}}{Hypotenuse}\text{ }\rightarrow\text{ Cosine(}\angle S)\text{ = }(6)/(7)`
`\text{ }\angle S\text{ = }\cos ^(-1)((6)/(7))`
`\angle S=31.002719^(\circ)`

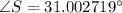
Rounding it to the nearest Tenth, we get:

`\angle S=31.002719^(\circ)=31.0^(\circ)`