Given:
The difference between the two numbers is 14.
Required:
We need to find the maximum or minimum value of the product of two numbers whose difference is 14.
Step-by-step explanation:
Let x be the first number.
The difference between the two numbers is 14.
The second number is x-14.
The product of the two numbers is
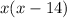
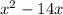
Differentiate this with respect to x and equate it to zero.

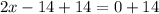
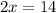
Divide both sides by 2.

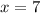
Substitute x =7 in the product.
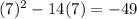
Final answer:
The maximum or minimum value of the product of two numbers whose difference is 14 is -49.