Question

the author selected 90 subjects from the california health survey and 52 were female construct and interpret a 99% confidence interval for the percentage of adult Californians that are female. round to the nearest hundredth place

Answer 1

`(52)/(90)=0.578`
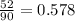
`\begin{gathered} 0.578\pm2.576\sqrt[]{((0.578)(1-0.578))/(90)}=0.578\pm0.13411 \\ (0.44,0.71) \end{gathered}`

The answer is this:

`(0.44389,0.71211)`

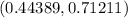
But we have to round those numbers to the nearest hundredth (two decimal places), so:

`\begin{gathered} 0.44389\approx0.44 \\ 0.71211\approx0.71 \end{gathered}`

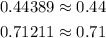
Therefore, the answer is :

`(0.44,0.71)`

a confidence interval for a population proportion is given by:

`\begin{gathered} p\pm Zc\sqrt[]{(p\cdot(1-p))/(n)} \\ \end{gathered}`

Some common confidence levels are:

`\begin{gathered} 90\colon Zc\approx1.645_{} \\ 95\colon Zc\approx1.960 \\ 99\colon Zc\approx2.576 \end{gathered}`

In this case:

`\begin{gathered} n=\text{ Sample size=90} \\ p=\text{proportion of females}=(52)/(90)\approx0.578 \end{gathered}`

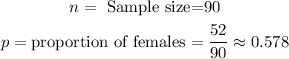
You replace those values into the equation, and you can find the confidence interval