Question

A point starts at the location (6,0) and travels 13.8 units CCW along a circle with a radius of 6 units that is centered at (0,0). Consider an angle whose vertex is at (0,0) and whose rays subtend the path that the point traveled. Draw a diagram of this to make sure you understand the context.What is the radian measure of this angle?______ radians   What is the degree measure of this angle? ____degrees

Answer 1

2.3 radians

131.78 degrees

Step-by-step explanation:

We can model the situation as follows:

So, the length of the arc formed by an angle θ in a circumference of radius = 6 units is 13.8 units.

Therefore, we can calculate θ in radians using the following equation:

`s=r\theta`

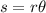
Where s is the length of the arc and r is the radius of the circle.

So, replacing the values and solving for θ, we get:

`\begin{gathered} 13.8=6\cdot\theta \\ (13.8)/(6)=(6\cdot\theta)/(6) \\ 2.3\text{ radians = }\theta \end{gathered}`

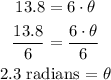
On the other hand, 3.14 radians are equivalent to 180 degrees, so 2.3 radians are equal to:

`2.3\text{ radians}*\frac{180\text{ degrees}}{3.14\text{ radians}}=131.78\text{ degrees}`

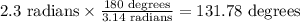
So, the measure of the angle is 2.3 radians and 131.78 degrees.