Question

Determine the slope m and y-intercept (if possible) of the linear equation(Pre-algebra)

Answer 1

`\begin{gathered} a)\text{ slope = -}(8)/(9) \\ b)\text{ Intercept \lparen x,y\rparen = \lparen0,}(1)/(9)) \\ c)\text{ E} \end{gathered}`

Step-by-step explanation:

The general equation of a straight line can be represented as:

`y\text{ = mx + b}`

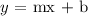
where m is the slope and b is the y-intercept

Now, let us rewrite the given equation in the form above:

`\begin{gathered} 9y\text{ = -8x + 1} \\ y\text{ = -}(8)/(9)x\text{ + }(1)/(9) \end{gathered}`

Now, from the above:

`\begin{gathered} slope\text{ = -}(8)/(9) \\ \\ y-intercept\text{ = }(1)/(9) \end{gathered}`

Now, let us describe the graph:

The graph will pass through the y-intercept

The y-intercept is at the point (0,1/9)

Hence, the graph passes through (0,1/9)

Furthermore, we can see that the slope is negative

This indicates a falling graph

This means the graph falls by 8 units vertically for every horizontal increase by 9 units