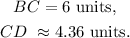Question

Use the diagram to help answer part A,B and C

Answer 1

Notice that angle B corresponds to one of the interior angles of triangle ADB and triangle CAB, since both triangles are right triangles, then by AA criterion

`\Delta ADB\approx\Delta CAB.`

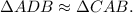
Now, we are given that the length of segment AC is 8 units and the length of segment AB is 10 units, since the triangles are right triangles, from the Pythagorean theorem we get that:

`BC^2+AC^2=AB^2.`

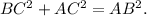
Solving the above equation for BC, we get:

`BC=√(AB^2-AC^2).`

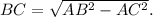
Therefore:

`BC=√(100u^2-64u^2)=√(36u^2)=6u.`

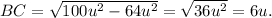
( u = units).

To find the length of CD, we will use the trigonometric function cosine:

`\begin{gathered} cos36^(\circ)=(AB)/(DB), \\ DB=(10u)/(cos36^(\circ))\approx12.36u. \end{gathered}`

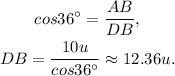
Finally, we get that:

`CD=DB-BC=12.36u-8u=4.36u.`

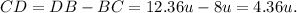
Answer:

a)

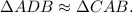
`\begin{equation*} \Delta ADB\approx\Delta CAB. \end{equation*}`

b)

`\begin{gathered} BC=6\text{ units,} \\ CD\text{ }\approx4.36\text{ units.} \end{gathered}`