A) The above figure is the label diagram of the jewelry box.
B) The equation of the volume will be,
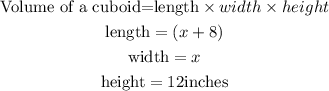
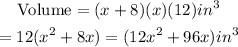
The equation for the volume of the box is (12x²+96x)in³.
C) To solve for the width of the box in metres, we will equate the equation of the volume to 240in³,

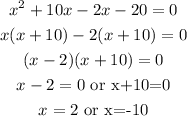
The width can never be negative, therefore the width is 2in.
Finally let us now convert the width to meters,
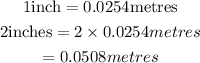
Hence, the width is 0.0508metres.