Question

I need to find the magnitude and direction angle of the resultant vector. This is different than what I am used to.

Answer 1

As given by the question

There are given that the point:

`\begin{gathered} P=(3,\text{ 3)} \\ Q=(9,\text{ -6)} \end{gathered}`

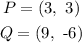
Now,

From the distance formula:

`PQ=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Then,

`\begin{gathered} PQ=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ PQ=\sqrt[]{(9_{}-3_{})^2+(-6_{}-3_{})^2} \\ PQ=\sqrt[]{(6)^2+(-9_{})^2} \end{gathered}`

Then,

`\begin{gathered} PQ=\sqrt[]{(6)^2+(-9_{})^2} \\ PQ=\sqrt[]{36^{}+81^{}} \\ PQ=\sqrt[]{117} \end{gathered}`

Now,

`\sqrt[]{3}PQ=\sqrt[]{3}*\sqrt[]{117}`

Then,

`\begin{gathered} \sqrt[]{3}PQ=\sqrt[]{3}*\sqrt[]{117} \\ =\sqrt[]{3}*3\sqrt[]{13} \\ =3\sqrt[]{39} \end{gathered}`

Hence, the answer is shown below:

`3\sqrt[]{39}`

Now,

From the formula to find the direction angle:

`\tan \theta=(y_2-y_1)/(x_2-x_1)`

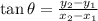
Then,

`\begin{gathered} \tan \theta=(y_2-y_1)/(x_2-x_1) \\ \tan \theta=\frac{-6_{}-3_{}}{9_{}-3_{}} \\ \tan \theta=\frac{-9_{}}{6_{}} \\ \theta=\tan ^(-1)(-(3)/(2)) \end{gathered}`

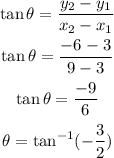
Then,

`\begin{gathered} \theta=\tan ^(-1)(-(3)/(2)) \\ \theta=-56.31^(\circ)+180^(\circ) \\ \theta=123.7 \end{gathered}`

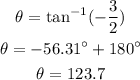
And

The magnitude of the point is:

`\begin{gathered} \lvert PQ\rvert=\lvert\sqrt[]{117}\rvert \\ \lvert PQ\rvert=\sqrt[]{117} \end{gathered}`

Hence, the value of direction angle and magnitude is shown below:

`\begin{gathered} \text{Direction angle=}\theta=123.7^(\circ)^{} \\ \text{Magnitude}=\sqrt[]{117} \end{gathered}`