Question

Systems of equations question. Thanks for your help, rubric and question linked below.

Answer 1

We are asked to determine the equation of an ellipse centered at the origin. To do that we will use the following general form of an ellipse equation:

`(x^2)/(a^2)+(y^2)/(b^2)=1`

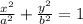
Where "a" is the interception with the x-axis and "b" is the interception with the y-axis. The vertical axis is the y-intercept and the minor axis is the x-intercept. Therefore, we have:

`\begin{gathered} b=8 \\ a=6 \end{gathered}`

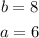
Substituting in the equation of the ellipse we get:

`(x^2)/(6^2)+(y^2)/(8^2)=1`

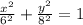
Solving the squares:

`(x^2)/(36)+(y^2)/(64)=1`

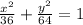
And thus we get the equation of the ellipse.

Part B. We are asked to determine the equation of a hyperbola. To do that we will use the general form of the equation of a hyperbola centered at the origin with a horizontal transverse axis is:

`(x^2)/(a^2)-(y^2)/(b^2)=1`

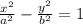
The value of "a" is the x-intercept. In the case of the given parabola we have:

`a=\pm4`

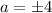
Substituting we get:

`(x^2)/((4)^2)-(y^2)/(b^2)=1`

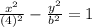
Solving the square:

`(x^2)/(16)-(y^2)/(b^2)=1`

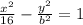
To determine the value of "b" we use the fact that the vertical asymptote in this type of hyperbolas is given by:

`y=\pm(b)/(a)x`

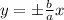
Since the given asymptote is:

`y=\pm(7)/(4)x`

This means that:

`(b)/(a)=(7)/(4)`

Since "a = 4":

`\begin{gathered} (b)/(4)=(7)/(4) \\ \\ b=7 \end{gathered}`

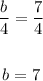
The value of "b" is 7. Substituting we get;

`(x^2)/(16)-(y^2)/(7^2)=1`

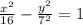
Solving the square:

`(x^2)/(16)-(y^2)/(49)=1`

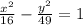
And thus we get the equation of the hyperbola.

Part C. A graph of the ellipse and the hyperbola is the following:

The domain of the function is the values of "x" that the function takes as input.

In the case of the ellipse, we notice that it takes values of "x" that are between -6 and 6, therefore, the domain of the ellipse is:

`D_(ellipse)=\lbrack-6,6\rbrack`

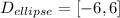
The hyperbola takes values between minus infinity and -4 and from 4 to infinity, therefore, the domain is:

`D_(hyperbola)=(-\infty,-4\rbrack\cup\lbrack4,\infty)`

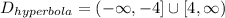
Since the domains have points in common and since the graph intercepts the system of equations does have a solution. The solutions are the interceptions between the graphs.