First, let's convert the area to m² and the charge to Coulomb:
13.08 cm² = 13.08 * 10^-4 m²
31.96 uC = 31.96 * 10^-6 C
The constant "eo" is the vacuum permittivity, equal to 8.85 * 10^-12.
So, calculating the electric field, we have:
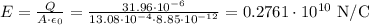
Now, to find the force acting on an electron, let's use the formula below, knowing that the charge of an electron is 1.6 * 10^-19 C:
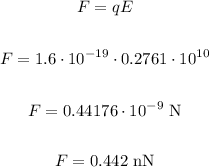
Therefore the force is 0.442 nanoNewtons.