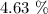Question

Suppose that the number of bacteria in a certain population Increases according to a continuous exponential growth model. A sample of 1300 bacteria selectedfrom this population reached the size of 1426bacteria in two hours. Find the hourly growth rate parameter.Note: This is a continuous exponential growth model.Write your answer as a percentage. Do not round any intermediate computations, and round your percentage to the nearest hundredth.

Answer 1

The equation of a continuous exponential growth model is:

`A=A_0\cdot e^(kt)`

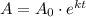
Where A represents the population at time t, A_0 represents the population at time t=0 and k is the hourly growth rate parameter.

Substitute A=1426, A_0=1300, and t=2:

`\Rightarrow1426=1300\cdot e^(2k)`

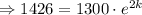
Solve for k:

`\begin{gathered} \Rightarrow(1426)/(1300)=e^(2k) \\ \Rightarrow\ln ((1426)/(1300))=2k \\ \Rightarrow(1)/(2)\ln ((1426)/(1300))=k \\ \Rightarrow k=(1)/(2)\ln ((1426)/(1300)) \end{gathered}`

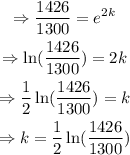
Use a calculator to find the value of k:

`\Rightarrow k=0.04625452876\ldots`

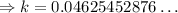
As a percentage, the value of k is 4.625...%

Therefore, to the nearest hundredth, the hourly growth rate parameter is:

`4.63\text{ \%}`