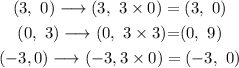Let y=f(x) is the original function and y=f(ax) is the new function, where a is a constant.
Then, y=f(ax) is a horizontal stretch or horizontal compression of f(x).
If a>1, then the graph of f(x) is compressed by 1/a.
If 0
The given function is y=f(x).
The new function is y=f(3x). It is of the form y=f(ax).
The constant 3 is greater than 1.
Therefore, the graph of y=f(3x) is the compression of the graph of f(x) by 1/3.
Identify some points on the graph of f(x) in the form (x, y).
(3, 0), (0, 3) and (-3, 0 ) are points on the graph of f(x).
Let (x', y') be a point on the graph of y=f(3x).
The transformation of each of the point on y=f(x) to y=f(3x) can be represented as,
(x, y)-->(x', y')-->(x/3, y).
For points (3, 0), (0, 3) and (-3, 0 ), the transformation can be described by ,