The general form of an arithmetic sequence can be written as:
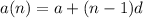
Where
a is the first term
d is the common difference [difference between a term and its preceeding term]
• The first term is 7
Thus,
a = 7
• The common difference between the terms is:
16 - 7 = 9
25 - 16 = 9
34 - 25 = 9
Thus,
common difference is 9
d = 9
Plugging into the equation we have:
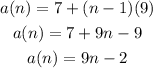
This question gives the information in a different notation, that's all.
We match it with our solution.
a(1), or f(1) is the first term, which is 7.
The formula given is in terms of f(n-1).
f(n-1) is the term before it
So, we have:
f(n) = term before it + WHAT???
We know that to get the next term [ f(n) }, we have to ADD 9 to the term before it [ f(n-1) ].
Thus,
f(n) = f(n-1) + 9
Looking at the answer choices, the last one is correct.
Correct Answer:
f(1) = 7; f(n) = f(n-1) + 9