Question

Find the lenghth of hypotonuse if one lengh is 6 , leave it simplified redical form

Answer 1

We are given a right triangle and we are asked to determine the length of the hypotenuse. To do that we will use the Pythagorean theorem:

`h^2=a^2+b^2`

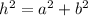
Where "h" is the hypothenuse and a and b the other two sides. In this case, the two sides are equal since the triangle is 45 - 45 - 90. We have the following values:

`\begin{gathered} a=6 \\ b=6 \end{gathered}`

Substituting:

`h^2=(6)^2+(6)^2`

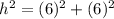
Solving the operations:

`\begin{gathered} h^2=36+36 \\ h^2=2(36) \end{gathered}`

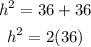
Taking square root to both sides:

`h=\sqrt[]{2(36)}`

Now we will use the following property:

`\sqrt[]{ab}=\sqrt[]{a}*\sqrt[]{b}`

Applying the property:

`h=\sqrt[]{2}*\sqrt[]{36}`

Solving the operations:

`h=6\sqrt[]{2}`

And thus we have found the hypothenuse in its most simplified form.