The rule of the simple interest is
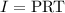
P is the initial value
R is the annual rate in decimal
T is the time in years
Since the annual rate is 3.6%, then
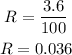
Since his loan is $15,600, then
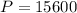
Since the time is 78 days, then

Substitute them in the rule above
a)

Round it to the nearest cents (2 decimal places)
I = $120.01
The interest will be $120.01
b)
To find the amount owed after 78 days add I and P
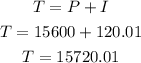
The amount owed after 78 days is $15720.01