Question

Use this to find the equation of the tangent line to the parabola

Answer 1

`\begin{gathered} f(x)=4x^2-2x+3 \\ (d)/(dx)f(x)=(d)/(dx)(4x^2-2x+3) \end{gathered}`

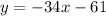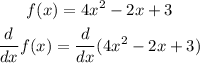
Applying the sum and difference rules:

`(d)/(dx)f(x)=(d)/(dx)(4x^2)-(d)/(dx)(2x)+(d)/(dx)(3)`

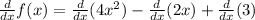
Applying the constant multiple rule:

`(d)/(dx)f(x)=4(d)/(dx)(x^2)-2(d)/(dx)(x)+(d)/(dx)(3)`

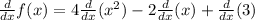
The derivative of a constant is zero, and the derivative of x is one. Applying the power rule:

`\begin{gathered} (d)/(dx)f(x)=4(2x^{})-2(1)+0 \\ f^(\prime)(x)=8x^{}-2 \end{gathered}`

Evaluating f'(x) at x = -4:

`\begin{gathered} f^(\prime)(-4)=8(-4)^{}-2 \\ f^(\prime)(-4)=-34 \end{gathered}`

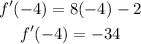
This value is the slope of the tangent line at the point (-4, 75), that is,

`m=-34`

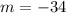
Given the general equation of a line:

`y=mx+b`

Substituting with m = -34 and the point (-4, 75), that is, x = -4, and y = 75, and solving for b:

`\begin{gathered} 75=(-34)(-4)+b \\ 75=136+b \\ 75-136=b \\ -61=b \end{gathered}`

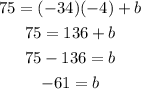
And the equation of the tangent line is:

`y=-34x-61`