We have
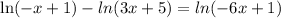
We need to simplify by applying logarithms rules
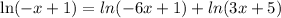
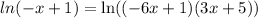
Then we apply the exponential on both sides
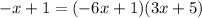
We simplify
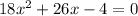
Then we solve the second equation degree with the general formula
![x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/li72dimqx1poek8bdg3bs589861h83kfxl.png)
where
a=18
b=26
c=-4
we substitute the values
![x_(1,2)=\frac{-26\pm\sqrt[]{(26)^2-4(18)(-4)}}{2(18)}](https://img.qammunity.org/2023/formulas/mathematics/college/iefsfrjz7bqzzhuriougwhhdb05eih3jy7.png)
![x_(1,2)=\frac{-26\pm2\sqrt[]{241}}{36}](https://img.qammunity.org/2023/formulas/mathematics/college/8jxjgiderk9x2ow23s3laygk18zfhy7rvw.png)
We reduce and the solution is
![x_1=\frac{-13+\sqrt[]{241}}{18}=0.14](https://img.qammunity.org/2023/formulas/mathematics/college/9g753h0s0q1dnd5ge6kzm5skny2tss5fl7.png)
![x_2=\frac{-13-\sqrt[]{241}}{18}=-1.58](https://img.qammunity.org/2023/formulas/mathematics/college/9tqspz6rnu1t4yoo8srd1iskl77fy1okfq.png)
ANSWER
–1.58 or 0.14