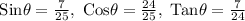Question

find the exact values of the three trigonomic functions of the angle 0 (sin 0, cos 0 and tan 0) in the figure.Use the Pythagorean theorem to find the third side of the triangle

Answer 1

In the given triangle we have, a = 7, b = 24

In right angle triangle we have, Perpendicular = 7 , base=24

Apply Pythagoras to find the Hypotenuse of the triangle:

Puthagoras Theorem:

In the right angle triangle, The sum of square of perpendicular and base is equal to the square of the hypotenuse.

Hypotenuse²= Base² + Perpendicular²

In the given figure we hvae to evaluate the hypotenuse

`\begin{gathered} \text{Hypotenuse}^2=perpendicular^2+base^2 \\ \text{Hypotenuse}^2=7^2+24^2 \\ \text{Hypotenuse}^2=49+576 \\ \text{Hypotenuse}^2=625 \\ \text{Hypotenuse}=\text{ 25} \end{gathered}`

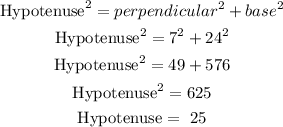
Hypotenuse =25

All sides are : 25, 7, 24

The ratio of Perpendicular to the base is the tangent.

`\begin{gathered} \text{Tan}\theta=(Perpendicular)/(Base) \\ \text{Tan}\theta=(a)/(b) \\ \text{Tan}\theta=(7)/(24) \\ \text{Tan}\theta=0.291 \\ \theta=\tan ^(-1)(0.291) \\ \theta=16.2^o \end{gathered}`

So, we get

`\begin{gathered} \text{For, Sin}\theta=(Perpendicular)/(Hypotenuse) \\ \text{ Sin}\theta=(7)/(25) \\ \\ \text{for Cos}\theta=(Base)/(Hypotenuse) \\ \text{Cos}\theta=(24)/(25) \end{gathered}`

thus, the trignometric ratio of angle is :

`\text{ Sin}\theta=(7)/(25),\text{ Cos}\theta=(24)/(25),\text{ Tan}\theta=(7)/(24)`

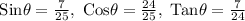
ANswer:

A)

`\text{ Sin}\theta=(7)/(25),\text{ Cos}\theta=(24)/(25),\text{ Tan}\theta=(7)/(24)`