Question

Graph the following function by hand and support your sketch with a calculator graph. Give the domain, range, and the equation of the asymptote. Determine if f is increasing or decreasing on its domain.f(x)=10^x

Answer 1

`\text{Domain}\colon x=(-\infty,\infty)`

`\text{Range}\colon(0,\infty)`
`\begin{gathered} f(x)=0 \\ 10^x=0 \end{gathered}`

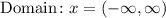
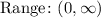
Step-by-step explanation:

Given the equation;

`f(x)=10^x`

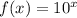
Graphing the function, let us find the value of f(x) at the various values of x;

`\begin{gathered} at\text{ x=0;} \\ f(0)=10^0=1 \\ at\text{ x=1;} \\ f(1)=10^1=10 \\ at\text{ x=2;} \\ f(2)=10^2=100 \\ at\text{ x=3;} \\ f(3)=10^3=1000 \end{gathered}`

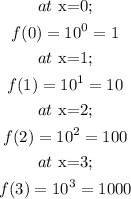
So, we have the points below on the graph;

`(0,1),(1,10),(2,100),(3,1000)`

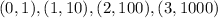
Graphing those points will give the graph of the function;

The domain of the function is the set of value of possible input (x) for the function;

`\text{Domain}\colon x=(-\infty,\infty)`

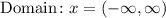
The Range of the function is is the set of value of possible output f(x) of the function;

`\text{Range}\colon(0,\infty)`

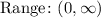
The function has an horizontal asymptote at;

`\begin{gathered} f(x)=0 \\ 10^x=0 \end{gathered}`

From the graph we can observe that the function increases as the value of x increases.

So, f(x) increases on its domain