For each table, we need to find if the table represents a linear or nonlinear function
If it is linear we can calculate a slope, otherwise, it is non-linear.
For the first table
x y
-2 4
0 6
2 9
for the first and second point
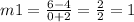
for the second and third point
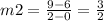
Because both the slopes are different, this table is non-linear
We need to do the same for each table. If they have different slopes the table is non-linear if they have equals slopes they are linear.
For
x y
-1 3
1 4
3 5
this one is linear
For
x y
1 -3
4 0
7 3
this one is linear
For
x y
3 -1
2 -2
4 -3
this one is non-linear
For
x y
1 -1
2 0
3 2
this one is non -linear
For
x y
-1 -2
-2 -4
-3 -6
this one is linear