SOLUTION
Out of the 828 tickets sold, some were student's tickets, while the rest were non-students tickets.
Let s represent student's tickets and n represent non-student tickets.
So that means s + n = 828 ......... equation 1
All the tickets were sold for $6279. Students' tickets sold for $6 and non-students' tickets sold for $9. This means that
6 x s + 9 x n = 6279
6s + 9n = 6279........... equation 2
So we will solve equations 1 and 2 simultaneously we have
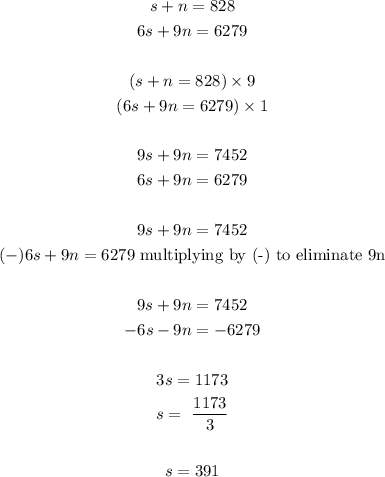
Therefore, the number of students tickets sold is 391